Elongated triangular cupola
| Elongated triangular cupola | |
|---|---|
 | |
| Type | Johnson J17 – J18 – J19 |
| Faces | 4 triangles 9 squares 1 hexagon |
| Edges | 27 |
| Vertices | 15 |
| Vertex configuration | 6(42.6) 3(3.4.3.4) 6(3.43) |
| Symmetry group | C3v |
| Dual polyhedron | - |
| Properties | convex |
| Net | |
 | |
In geometry, the elongated triangular cupola is a polyhedron constructed from a hexagonal prism by attaching a triangular cupola. It is an example of a Johnson solid.
Construction[edit]
The elongated triangular cupola is constructed from a hexagonal prism by attaching a triangular cupola onto one of its bases, a process known as the elongation.[1] This cupola covers the hexagonal face so that the resulting polyhedron has four equilateral triangles, nine squares, and one regular hexagon.[2] A convex polyhedron in which all of the faces are regular polygons is the Johnson solid. The elongated triangular cupola is one of them, enumerated as the eighteenth Johnson solid .[3]
Properties[edit]
The surface area of an elongated triangular cupola is the sum of all polygonal face's area. The volume of an elongated triangular cupola can be ascertained by dissecting it into a cupola and a hexagonal prism, after which summing their volume. Given the edge length , its surface and volume can be formulated as:[2]

It has the three-dimensional same symmetry as the triangular cupola, the cyclic group of order 6. Its dihedral angle can be calculated by adding the angle of a triangular cupola and a hexagonal prism:[4]
- the dihedral angle of an elongated triangular cupola between square-to-triangle is that of a triangular cupola between those: 125.3°;
- the dihedral angle of an elongated triangular cupola between two adjacent squares is that of a hexagonal prism, the internal angle of its base 120°;
- the dihedral angle of a hexagonal prism between square-to-hexagon is 90°, that of a triangular cupola between square-to-hexagon is 54.7°, and that of a triangular cupola between triangle-to-hexagonal is an 70.5°. Therefore, the elongated triangular cupola between square-to-square and triangle-to-square, on the edge where a triangular cupola is attached to a hexagonal prism, is 90° + 54.7° = 144.7° and 90° + 70.5° = 166.5° respectively.
Dual polyhedron[edit]
The dual of the elongated triangular cupola has 15 faces: 6 isosceles triangles, 3 rhombi, and 6 quadrilaterals.
| Dual elongated triangular cupola | Net of dual |
|---|---|
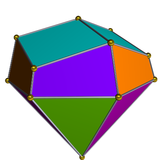
|

|
Related polyhedra and honeycombs[edit]
The elongated triangular cupola can form a tessellation of space with tetrahedra and square pyramids.[5]
References[edit]
- ^ Rajwade, A. R. (2001), Convex Polyhedra with Regularity Conditions and Hilbert's Third Problem, Texts and Readings in Mathematics, Hindustan Book Agency, p. 84–89, doi:10.1007/978-93-86279-06-4, ISBN 978-93-86279-06-4.
- ^ a b Berman, Martin (1971), "Regular-faced convex polyhedra", Journal of the Franklin Institute, 291 (5): 329–352, doi:10.1016/0016-0032(71)90071-8, MR 0290245.
- ^ Francis, Darryl (August 2013), "Johnson solids & their acronyms", Word Ways, 46 (3): 177.
- ^ Johnson, Norman W. (1966), "Convex polyhedra with regular faces", Canadian Journal of Mathematics, 18: 169–200, doi:10.4153/cjm-1966-021-8, MR 0185507, S2CID 122006114, Zbl 0132.14603.
- ^ "J18 honeycomb".





